Creating an advanced model setup¶
Note
This guide is still work in progress.
This is a step-by-step guide that illustrates how even complicated setups can be created with relative ease (thanks to the tools provided by the scientific Python community). As an example, we will re-create the wave propagation setup, which is a global ocean model with an idealized Atlantic.
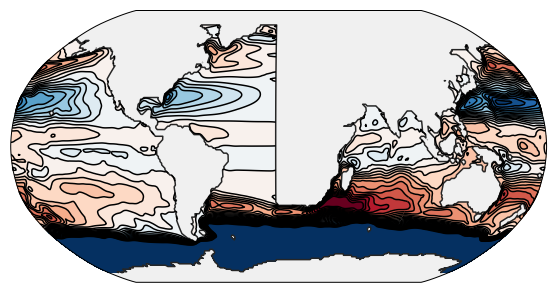
The resulting stream function after about 1 year of integration.¶
The vision¶
The purpose of this model is to examine wave propagation along the eastern boundary of the North Atlantic. Since it is difficult to track propagating waves along ragged geometry or through uneven forcing fields, we will idealize the representation of the North Atlantic; and as the presence of the Pacific in the model is crucial to achieve a realistic ocean circulation, we want to use a global model.
This leaves us with the following requirements for the final wave propagation model:
A global model with a resolution of around 2 degrees and meridional stretching.
Convert the eastern boundary of the Atlantic to a straight line, so analytically derived wave properties hold.
A refined grid resolution at the eastern boundary of the Atlantic.
Zonally averaged forcings in the Atlantic.
A somehow interpolated initial state for cells that have been converted from land to ocean in the North Atlantic.
Options for shelf and continental slope.
A multiplier setting for the Southern Ocean wind stress.
Model skeleton¶
Instead of starting from scratch, we can use the global one degree model as a template, which looks like this:
#!/usr/bin/env python
import os
import h5netcdf
from veros import VerosSetup, tools, veros_method, time
from veros.variables import Variable, allocate
BASE_PATH = os.path.dirname(os.path.realpath(__file__))
DATA_FILES = tools.get_assets('global_1deg', os.path.join(BASE_PATH, 'assets.yml'))
class GlobalOneDegreeSetup(VerosSetup):
"""Global 1 degree model with 115 vertical levels.
`Adapted from pyOM2 <https://wiki.zmaw.de/ifm/TO/pyOM2/1x1%20global%20model>`_.
"""
@veros_method
def set_parameter(self, vs):
"""
set main parameters
"""
vs.nx = 360
vs.ny = 160
vs.nz = 115
vs.dt_mom = 1800.0
vs.dt_tracer = 1800.0
vs.runlen = 0.
vs.coord_degree = True
vs.enable_cyclic_x = True
vs.congr_epsilon = 1e-10
vs.congr_max_iterations = 10000
vs.enable_hor_friction = True
vs.A_h = 5e4
vs.enable_hor_friction_cos_scaling = True
vs.hor_friction_cosPower = 1
vs.enable_tempsalt_sources = True
vs.enable_implicit_vert_friction = True
vs.eq_of_state_type = 5
# isoneutral
vs.enable_neutral_diffusion = True
vs.K_iso_0 = 1000.0
vs.K_iso_steep = 50.0
vs.iso_dslope = 0.005
vs.iso_slopec = 0.005
vs.enable_skew_diffusion = True
# tke
vs.enable_tke = True
vs.c_k = 0.1
vs.c_eps = 0.7
vs.alpha_tke = 30.0
vs.mxl_min = 1e-8
vs.tke_mxl_choice = 2
vs.kappaM_min = 2e-4
vs.kappaH_min = 2e-5
vs.enable_kappaH_profile = True
vs.enable_tke_superbee_advection = True
# eke
vs.enable_eke = True
vs.eke_k_max = 1e4
vs.eke_c_k = 0.4
vs.eke_c_eps = 0.5
vs.eke_cross = 2.
vs.eke_crhin = 1.0
vs.eke_lmin = 100.0
vs.enable_eke_superbee_advection = True
vs.enable_eke_isopycnal_diffusion = True
# idemix
vs.enable_idemix = False
vs.enable_eke_diss_surfbot = True
vs.eke_diss_surfbot_frac = 0.2
vs.enable_idemix_superbee_advection = True
vs.enable_idemix_hor_diffusion = True
# custom variables
vs.nmonths = 12
vs.variables.update(
t_star=Variable('t_star', ('xt', 'yt', 'nmonths'), '', '', time_dependent=False),
s_star=Variable('s_star', ('xt', 'yt', 'nmonths'), '', '', time_dependent=False),
qnec=Variable('qnec', ('xt', 'yt', 'nmonths'), '', '', time_dependent=False),
qnet=Variable('qnet', ('xt', 'yt', 'nmonths'), '', '', time_dependent=False),
qsol=Variable('qsol', ('xt', 'yt', 'nmonths'), '', '', time_dependent=False),
divpen_shortwave=Variable('divpen_shortwave', ('zt',), '', '', time_dependent=False),
taux=Variable('taux', ('xt', 'yt', 'nmonths'), '', '', time_dependent=False),
tauy=Variable('tauy', ('xt', 'yt', 'nmonths'), '', '', time_dependent=False),
)
@veros_method
def _read_forcing(self, vs, var):
with h5netcdf.File(DATA_FILES['forcing'], 'r') as infile:
var = infile.variables[var]
return np.array(var, dtype=str(var.dtype)).T
@veros_method
def set_grid(self, vs):
dz_data = self._read_forcing(vs, 'dz')
vs.dzt[...] = dz_data[::-1]
vs.dxt[...] = 1.0
vs.dyt[...] = 1.0
vs.y_origin = -79.
vs.x_origin = 91.
@veros_method
def set_coriolis(self, vs):
vs.coriolis_t[...] = 2 * vs.omega * np.sin(vs.yt[np.newaxis, :] / 180. * vs.pi)
@veros_method(dist_safe=False, local_variables=['kbot'])
def set_topography(self, vs):
bathymetry_data = self._read_forcing(vs, 'bathymetry')
salt_data = self._read_forcing(vs, 'salinity')[:, :, ::-1]
mask_salt = salt_data == 0.
vs.kbot[2:-2, 2:-2] = 1 + np.sum(mask_salt.astype(np.int), axis=2)
mask_bathy = bathymetry_data == 0
vs.kbot[2:-2, 2:-2][mask_bathy] = 0
vs.kbot[vs.kbot >= vs.nz] = 0
# close some channels
i, j = np.indices((vs.nx, vs.ny))
mask_channel = (i >= 207) & (i < 214) & (j < 5) # i = 208,214; j = 1,5
vs.kbot[2:-2, 2:-2][mask_channel] = 0
# Aleutian islands
mask_channel = (i == 104) & (j == 134) # i = 105; j = 135
vs.kbot[2:-2, 2:-2][mask_channel] = 0
# Engl channel
mask_channel = (i >= 269) & (i < 271) & (j == 130) # i = 270,271; j = 131
vs.kbot[2:-2, 2:-2][mask_channel] = 0
@veros_method(dist_safe=False, local_variables=[
't_star', 's_star', 'qnec', 'qnet', 'qsol', 'divpen_shortwave', 'taux', 'tauy',
'temp', 'salt', 'forc_iw_bottom', 'forc_iw_surface', 'kbot', 'maskT', 'maskW',
'zw', 'dzt'
])
def set_initial_conditions(self, vs):
rpart_shortwave = 0.58
efold1_shortwave = 0.35
efold2_shortwave = 23.0
# initial conditions
temp_data = self._read_forcing(vs, 'temperature')
vs.temp[2:-2, 2:-2, :, 0] = temp_data[..., ::-1] * vs.maskT[2:-2, 2:-2, :]
vs.temp[2:-2, 2:-2, :, 1] = temp_data[..., ::-1] * vs.maskT[2:-2, 2:-2, :]
salt_data = self._read_forcing(vs, 'salinity')
vs.salt[2:-2, 2:-2, :, 0] = salt_data[..., ::-1] * vs.maskT[2:-2, 2:-2, :]
vs.salt[2:-2, 2:-2, :, 1] = salt_data[..., ::-1] * vs.maskT[2:-2, 2:-2, :]
# wind stress on MIT grid
vs.taux[2:-2, 2:-2, :] = self._read_forcing(vs, 'tau_x')
vs.tauy[2:-2, 2:-2, :] = self._read_forcing(vs, 'tau_y')
qnec_data = self._read_forcing(vs, 'dqdt')
vs.qnec[2:-2, 2:-2, :] = qnec_data * vs.maskT[2:-2, 2:-2, -1, np.newaxis]
qsol_data = self._read_forcing(vs, 'swf')
vs.qsol[2:-2, 2:-2, :] = -qsol_data * vs.maskT[2:-2, 2:-2, -1, np.newaxis]
# SST and SSS
sst_data = self._read_forcing(vs, 'sst')
vs.t_star[2:-2, 2:-2, :] = sst_data * vs.maskT[2:-2, 2:-2, -1, np.newaxis]
sss_data = self._read_forcing(vs, 'sss')
vs.s_star[2:-2, 2:-2, :] = sss_data * vs.maskT[2:-2, 2:-2, -1, np.newaxis]
if vs.enable_idemix:
tidal_energy_data = self._read_forcing(vs, 'tidal_energy')
mask = np.maximum(0, vs.kbot[2:-2, 2:-2] - 1)[:, :, np.newaxis] == np.arange(vs.nz)[np.newaxis, np.newaxis, :]
tidal_energy_data[:, :] *= vs.maskW[2:-2, 2:-2, :][mask].reshape(vs.nx, vs.ny) / vs.rho_0
vs.forc_iw_bottom[2:-2, 2:-2] = tidal_energy_data
wind_energy_data = self._read_forcing(vs, 'wind_energy')
wind_energy_data[:, :] *= vs.maskW[2:-2, 2:-2, -1] / vs.rho_0 * 0.2
vs.forc_iw_surface[2:-2, 2:-2] = wind_energy_data
"""
Initialize penetration profile for solar radiation and store divergence in divpen
note that pen is set to 0.0 at the surface instead of 1.0 to compensate for the
shortwave part of the total surface flux
"""
swarg1 = vs.zw / efold1_shortwave
swarg2 = vs.zw / efold2_shortwave
pen = rpart_shortwave * np.exp(swarg1) + (1.0 - rpart_shortwave) * np.exp(swarg2)
pen[-1] = 0.
vs.divpen_shortwave = allocate(vs, ('zt',))
vs.divpen_shortwave[1:] = (pen[1:] - pen[:-1]) / vs.dzt[1:]
vs.divpen_shortwave[0] = pen[0] / vs.dzt[0]
@veros_method
def set_forcing(self, vs):
t_rest = 30. * 86400.
cp_0 = 3991.86795711963 # J/kg /K
year_in_seconds = time.convert_time(1., 'years', 'seconds')
(n1, f1), (n2, f2) = tools.get_periodic_interval(vs.time, year_in_seconds,
year_in_seconds / 12., 12)
# linearly interpolate wind stress and shift from MITgcm U/V grid to this grid
vs.surface_taux[:-1, :] = f1 * vs.taux[1:, :, n1] + f2 * vs.taux[1:, :, n2]
vs.surface_tauy[:, :-1] = f1 * vs.tauy[:, 1:, n1] + f2 * vs.tauy[:, 1:, n2]
if vs.enable_tke:
vs.forc_tke_surface[1:-1, 1:-1] = np.sqrt((0.5 * (vs.surface_taux[1:-1, 1:-1] \
+ vs.surface_taux[:-2, 1:-1]) / vs.rho_0) ** 2
+ (0.5 * (vs.surface_tauy[1:-1, 1:-1] \
+ vs.surface_tauy[1:-1, :-2]) / vs.rho_0) ** 2) ** (3. / 2.)
# W/m^2 K kg/J m^3/kg = K m/s
t_star_cur = f1 * vs.t_star[..., n1] + f2 * vs.t_star[..., n2]
vs.qqnec = f1 * vs.qnec[..., n1] + f2 * vs.qnec[..., n2]
vs.qqnet = f1 * vs.qnet[..., n1] + f2 * vs.qnet[..., n2]
vs.forc_temp_surface[...] = (vs.qqnet + vs.qqnec * (t_star_cur - vs.temp[..., -1, vs.tau])) \
* vs.maskT[..., -1] / cp_0 / vs.rho_0
s_star_cur = f1 * vs.s_star[..., n1] + f2 * vs.s_star[..., n2]
vs.forc_salt_surface[...] = 1. / t_rest * \
(s_star_cur - vs.salt[..., -1, vs.tau]) * vs.maskT[..., -1] * vs.dzt[-1]
# apply simple ice mask
mask1 = vs.temp[:, :, -1, vs.tau] * vs.maskT[:, :, -1] <= -1.8
mask2 = vs.forc_temp_surface <= 0
ice = ~(mask1 & mask2)
vs.forc_temp_surface *= ice
vs.forc_salt_surface *= ice
# solar radiation
if vs.enable_tempsalt_sources:
vs.temp_source[..., :] = (f1 * vs.qsol[..., n1, None] + f2 * vs.qsol[..., n2, None]) \
* vs.divpen_shortwave[None, None, :] * ice[..., None] \
* vs.maskT[..., :] / cp_0 / vs.rho_0
@veros_method
def set_diagnostics(self, vs):
average_vars = ['surface_taux', 'surface_tauy', 'forc_temp_surface', 'forc_salt_surface',
'psi', 'temp', 'salt', 'u', 'v', 'w', 'Nsqr', 'Hd', 'rho',
'K_diss_v', 'P_diss_v', 'P_diss_nonlin', 'P_diss_iso', 'kappaH']
if vs.enable_skew_diffusion:
average_vars += ['B1_gm', 'B2_gm']
if vs.enable_TEM_friction:
average_vars += ['kappa_gm', 'K_diss_gm']
if vs.enable_tke:
average_vars += ['tke', 'Prandtlnumber', 'mxl', 'tke_diss',
'forc_tke_surface', 'tke_surf_corr']
if vs.enable_idemix:
average_vars += ['E_iw', 'forc_iw_surface', 'forc_iw_bottom', 'iw_diss',
'c0', 'v0']
if vs.enable_eke:
average_vars += ['eke', 'K_gm', 'L_rossby', 'L_rhines']
vs.diagnostics['averages'].output_variables = average_vars
vs.diagnostics['cfl_monitor'].output_frequency = 86400.0
vs.diagnostics['snapshot'].output_frequency = 365 * 86400 / 24.
vs.diagnostics['overturning'].output_frequency = 365 * 86400
vs.diagnostics['overturning'].sampling_frequency = 365 * 86400 / 24.
vs.diagnostics['energy'].output_frequency = 365 * 86400
vs.diagnostics['energy'].sampling_frequency = 365 * 86400 / 24.
vs.diagnostics['averages'].output_frequency = 365 * 86400
vs.diagnostics['averages'].sampling_frequency = 365 * 86400 / 24.
@veros_method
def after_timestep(self, vs):
pass
@tools.cli
def run(*args, **kwargs):
simulation = GlobalOneDegreeSetup(*args, **kwargs)
simulation.setup()
simulation.run()
if __name__ == '__main__':
run()
The biggest changes in the new wave propagation setup will be located in the
set_grid() set_topography() and set_initial_conditions()
methods to accommodate for the new geometry and the interpolation of initial
conditions to the modified grid, so we can concentrate on implementing those
first.
Step 1: Setup grid¶
Warning
When using a non-uniform grid,
Step 2: Create idealized topography¶
Usually, to create an idealized topography, one would simply hand-craft some input and forcing files that reflect the desired changes. However, since we want our setup to have flexible resolution, we will have to write an algorithm that creates these input files for any given number of grid cells. One convenient way to achieve this is by creating some high-resolution masks representing the target topography by hand, and then interpolate these masks to the desired resolution.
Create a mask image¶
Before we can start, we need to download a high-resolution topography dataset. There are many freely available topographical data sets on the internet; one of them is ETOPO5 (with a resolution of 5 arc-minutes), which we will be using throughout this tutorial. To create a mask image from the topography file, you can use the command line tool veros create-mask, e.g. like
$ veros create-mask ETOPO5_Ice_g_gmt4.nc
This creates a one-to-one representation of the topography file as a PNG image. However, in the case of the 5 arc-minute topography, the resulting image includes a lot of small islands and complicated coastlines that might cause problems when being interpolated to a numerical grid with a much lower resolution. To address this, the create-mask script accepts a scale argument. When given, a Gaussian filter with standard deviation scale (in grid cells) is applied to the resulting image, smoothing out small features. The command
$ veros create-mask ETOPO5_Ice_g_gmt4 --scale 3 3
results in the following mask:
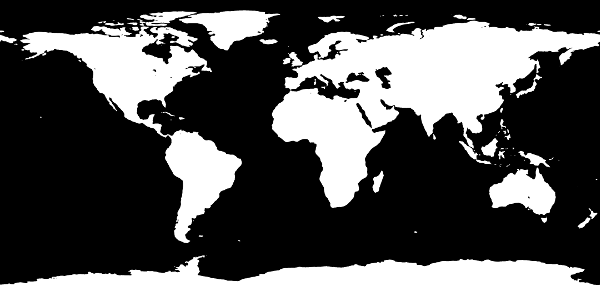
Smoothed topography mask¶
which looks good enough to serve as a basis for horizontal resolutions of around one degree.
Modify the mask¶
We can now proceed to mold this realistic version of the global topography into the desired idealized shape. You can use any image editor you have available; one possibility is the free software GIMP. Inside the editor, we can use the pencil tools to create a modified version of the topography mask:
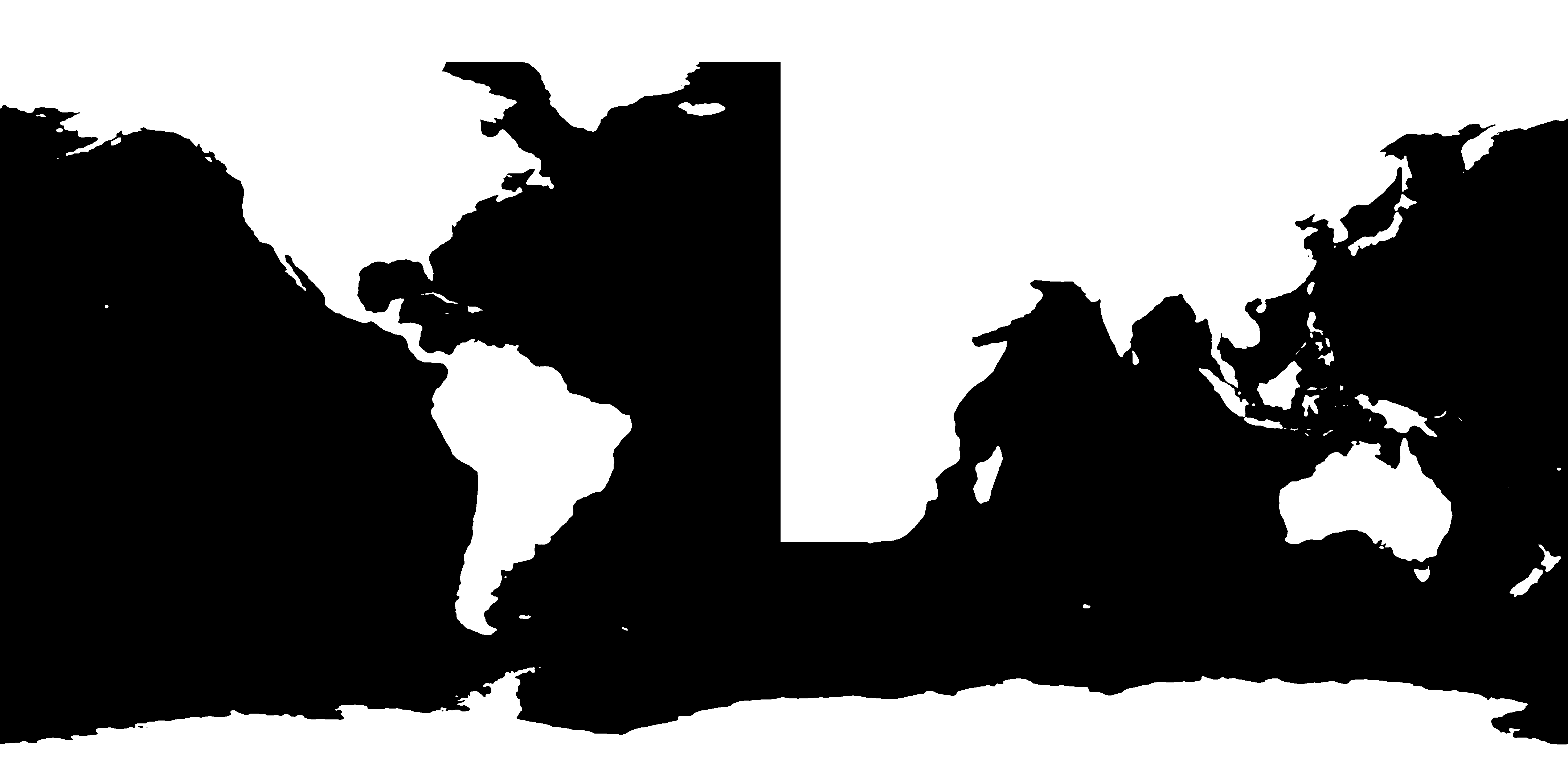
Idealized topography mask¶
In this modified version, I have
replaced the eastern boundary of the North Atlantic by a meridional line;
removed all lakes and inland seas;
thickened Central America (to prevent North and South America to become disconnected due to interpolation artifacts); and
removed the Arctic Ocean and Hudson Bay.
Now that our topography mask is finished, we can go ahead and implement it in the Veros setup!
Import to Veros¶
To read the mask in PNG format, we are going to use the Python Imaging Library (PIL).
Step 3: Interpolate forcings & initial conditions¶
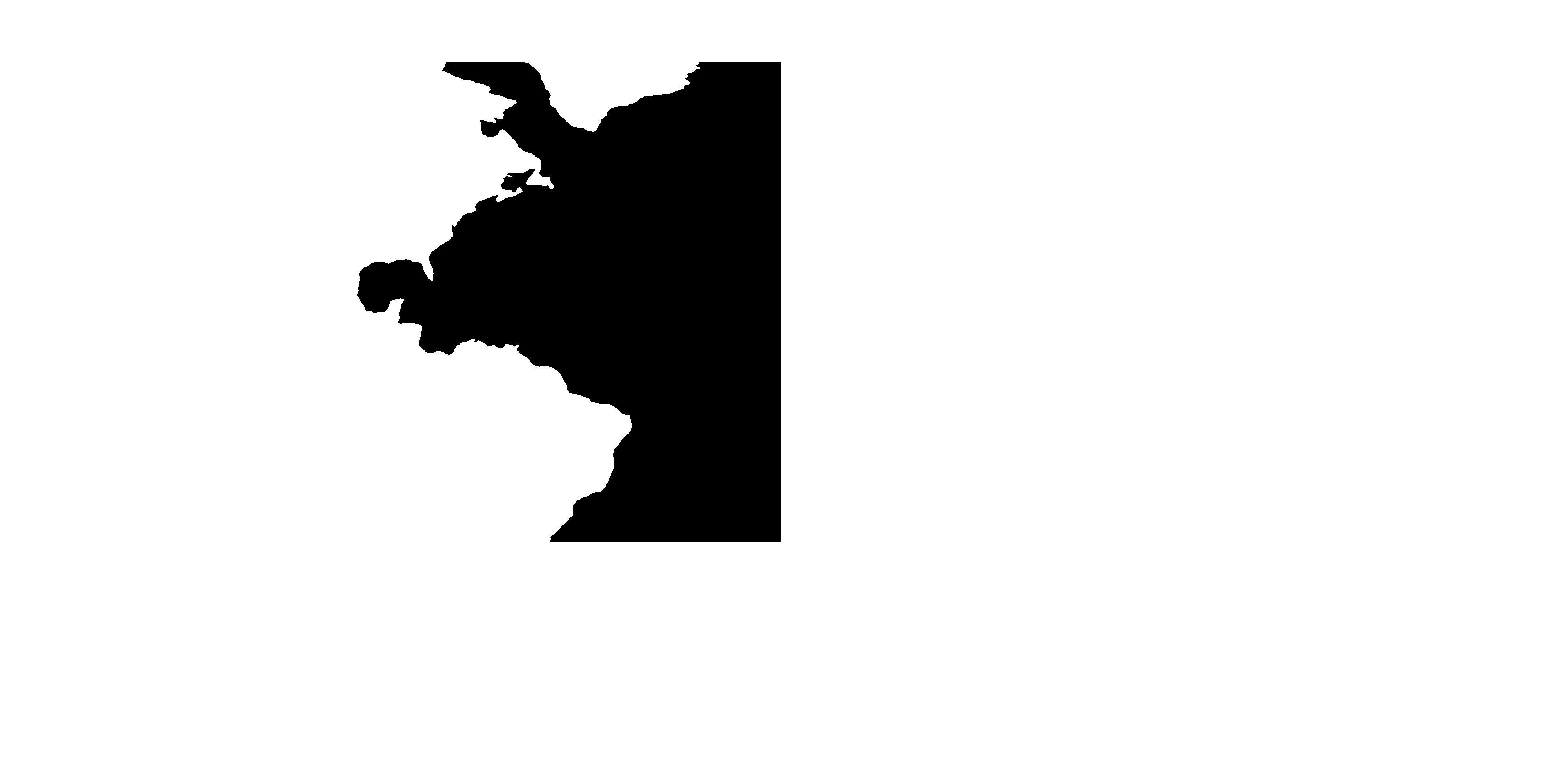
Mask to identify grid cells in the North Atlantic¶